0과 1 사이 값으로 파이 계산하기

예전에 우연히 발견하고 재밌게 풀었던 문젠데, 파이 데이라 다시 생각나서 정리해서 올려봅니다.

Q. random()이란 함수는 0과 1 사이의 실수를 무작위로 리턴합니다. 이때 파이(PI)의 값을 구하시오. (단, random()의 리턴값은 0과 1 사이에서 연속 균등확률분포를 따른다.)

기억나는 대로 문제를 적어봤습니다.
괄호 안의 조건은 코드로 구현하기 힘드니, 풀이가 완벽해도 결과가 정확하지 않을 수 있습니다.

풀 생각이 있으시면 여기서 스크롤을 멈추시면 됩니다.
아래엔 혹여 풀이 과정이 보일까 싶어 이미지 하나 넣어두겠습니다.

풀이

파이(원주율)은 원의 지름에 대한 원주(원둘레)의 비입니다.
2차원의 공간에서 만드는 값을 계산해야 하니, 루프 내부에서 random()을 두 번씩 호출해 (random(), random()) 위치에 점을 찍으면

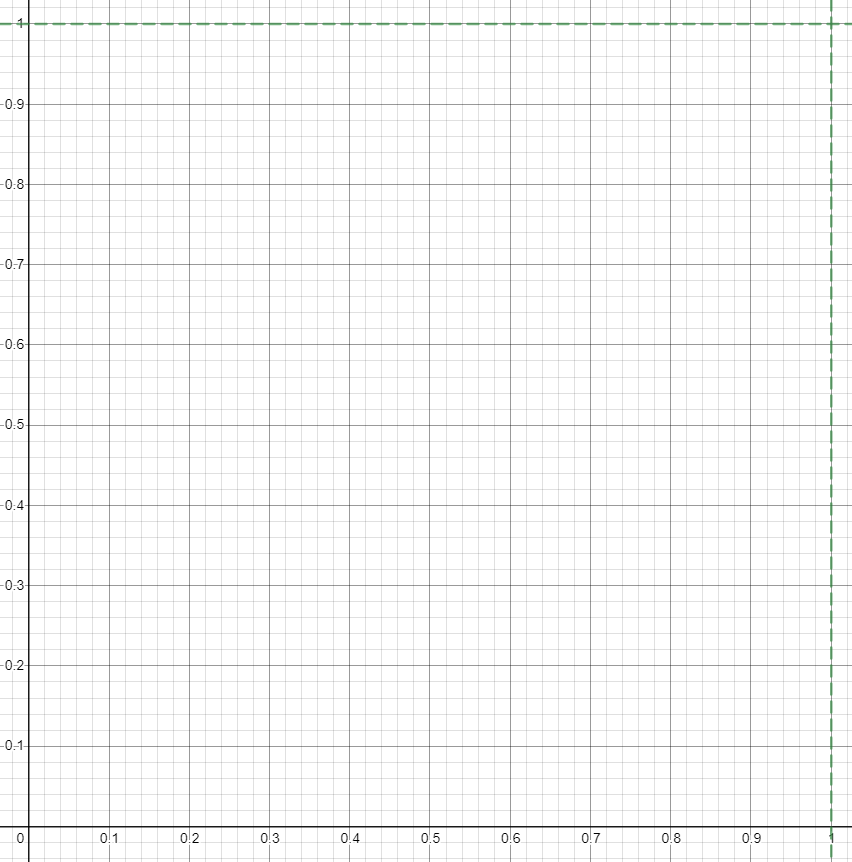
모든 점은 이 안에 있을 겁니다.

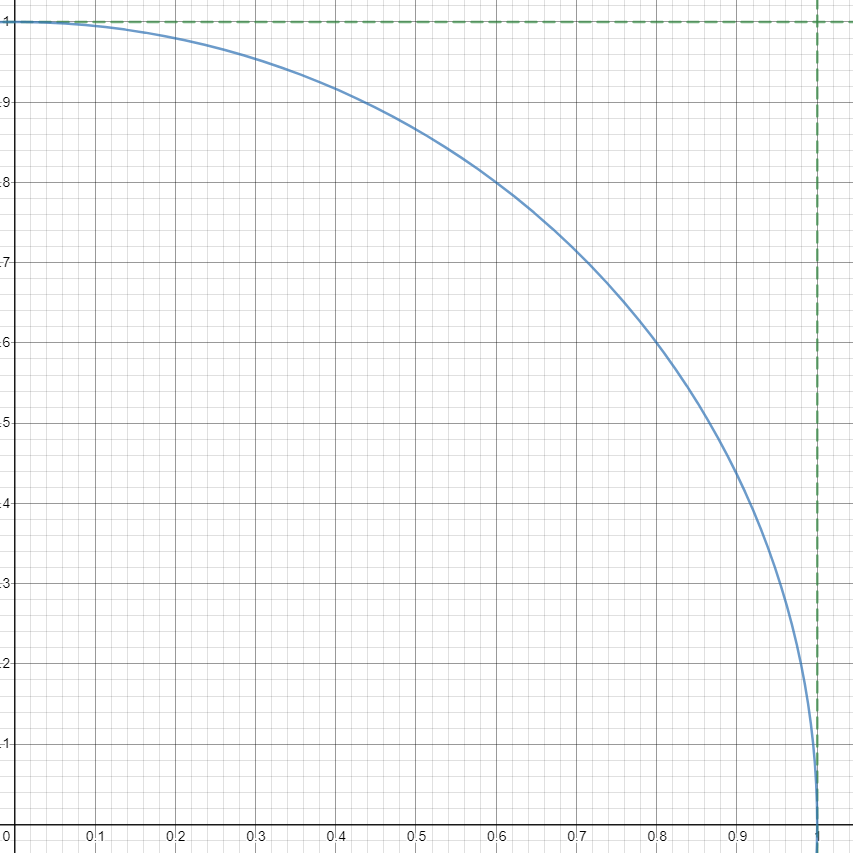
점이 (0, 0)에서 (1, 1) 사이의 모든 공간에 존재할 확률이 같다면,
파란 호의 너비 : 초록 정사각형의 너비 = 파란 호 내부의 점 : 초록 정사각형 내부의 점일 겁니다.

정리하면, 1 / 4 * PI : 1 = 파란 호 내부의 점 : 초록 정사각형 내부의 점입니다.
이를 정리하면, PI = 4 * 파란 호 내부의 점 / 초록 정사각형 내부의 점입니다.

원은 한 정점으로부터 같은 거리만큼 떨어진 점의 집합이니, 점이 파란 호 내부에 있는지 확인하려면 점과 원점의 거리가 1 이하인지 확인하면 됩니다.
피타고라스의 정리로 좌표평면에서 두 점 사이의 거리는 √(x2 - x1) ^ 2 + (y2 - y1) ^ 2입니다.
x1과 y1이 0이니, 루프 안에서 저희가 계산해야 할 건 √random()^2 + random()^2가 1 이하인지 확인하면 됩니다.

이를 자바스크립트로 정리하면

const { random } = Math;
 
function generateCoords() {
    const max = 100000;
    let inCircle = 0;
 
    for (let i = 1; i < max; i++) {
        const randomCoordDistance = Math.sqrt(
            Math.pow(random(), 2) + Math.pow(random(), 2)
        );
 
        randomCoordDistance <= 1 && inCircle++;
    }
 
    return (4 * inCircle) / max; // PI
}

Math.random()은 0과 1 사이의 실수를 반환하는 이 문제에 딱 어울리는 함수입니다.
Math.sqrt(숫자)는 숫자의 제곱근을 반환하고, Math.pow(숫자1, 숫자2)는 숫자1 ^ 숫자2를 반환합니다.

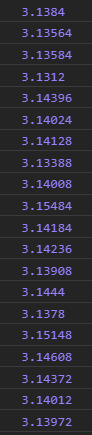
Math.random()이 제멋대로인 탓에 파이를 완벽히 계산할 순 없지만, 근삿값을 얻을 수 있었습니다.

물론 이런 거 다 필요없이 Math.PI 하면 파이를 반환해줍니다.